What is Big-O Notation?
Nutshell: Describes how an algorithm scales with increased input data
“Big O notation is used in Computer Science to describe the performance or complexity of an algorithm. Big O specifically describes the worst-case scenario, and can be used to describe the execution time required or the space used (e.g. in memory or on disk) by an algorithm.” -Rob Bell
Complexity Levels
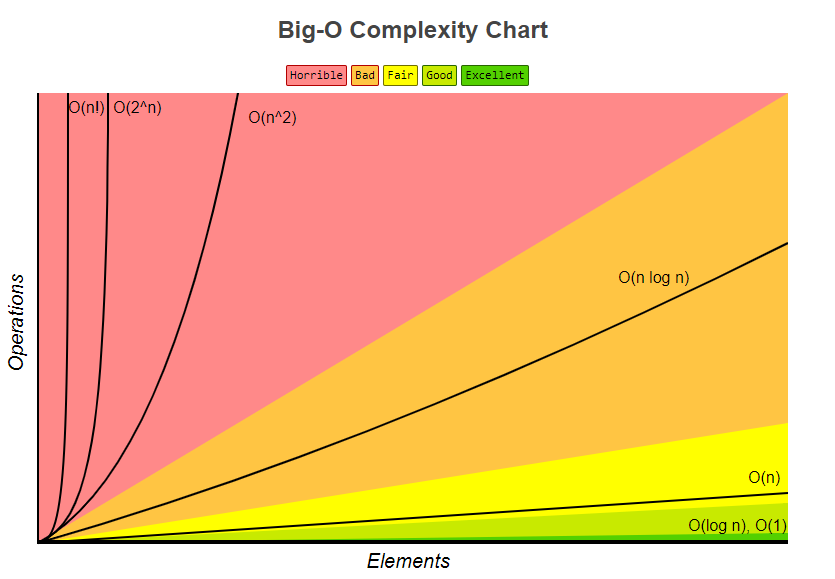
Chart from http://bigocheatsheet.com/
Common Performance Constants
| O(1) | Constant Time | Constant time regardless of data set size “The input array could be 1 item or 1,000 items, but this function would still just require one ‘step.'” |
| O(LogN) | Logarithmic | Performance has a slow decrease as the data set gets larger. Usually when using Divide and Conquer algorithms or data structure like trees, where the depth of the tree grows slower than the amount of data |
| O(N) | Linear Time | Performance changes linearly in proportion to the size of the data set. “If the array has 10 items, we have to print 10 times. If it has 1,000 items, we have to print 1,000 times.” |
| O(NLogN) | Log Linear | Performance slows down as the data set gets larger. Typical performance of good sorting algorithms (Merge Sort, Quick Sort, Heap Sort) |
| O(N2), O(N3), O(Nx) | Quadratic Time, Cubic Time, |
Performance grinds to a halt as data set gets larger. This tends to happen with nested loops that compare “every” item. We can usually see `x` nested loops in the algorithm “If the array has 10 items, we have to print 100 times. If it has 1,000 items, we have to print 1,000,000 times.” Nx (bubble sort, insertion sort, number of handshakes in a room…) |
| O(2N) | Exponential Time, Combination time |
Combination Loops – looking at various subsets in the input 2N Tower of Hanoi, |
| O(N!) | Permutation O | This algorithm iterates over all possible combinations of the inputs Example: traveling salesman |
How do Data Structures and Algorithms Perform?
See http://bigocheatsheet.com/ for charts of the relative performance of different data structures and sort algorithms.
Best, Average, Worst
Sometimes, in addition to using big-Θ (Big-O) to represent the upper-bound or worst-case performance we also use Big-θ (Big-Theta) notation to represent the average case performance, and Big-Ω (Big-Omega) notation to represent the best case or performance lower-bound.
